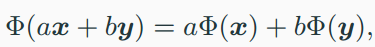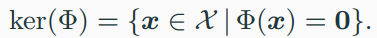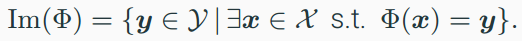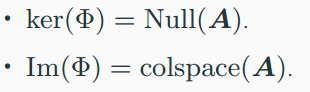본 포스팅은 AI501 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

행렬 곱셈

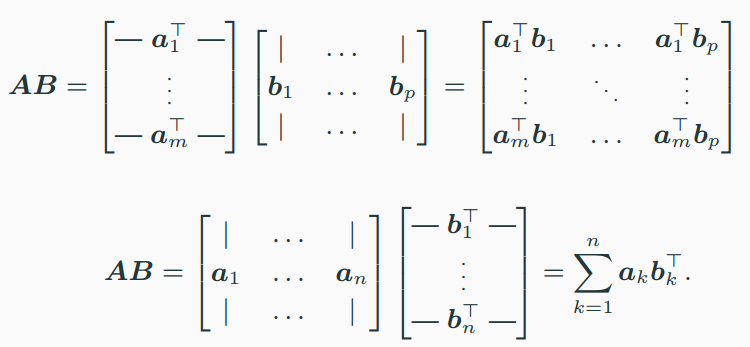
아래 그림과 같이 행렬의 곱셈을 할 때

• 행 벡터 x 열 벡터 하면 outer product 처럼 됨.
• 열 벡터 x 행 벡터 하면 inner product의 sum 처럼 됨.

• covariance matrix

위 내용은 covariance matrix를 계산할 때 유용하게 사용할 수 있다.

x = {x1, x2, … , xn} (여기서 xi는 열벡터이다.)일 때, covariance matrix는 $\frac{1}{n}\sum{x_i{x_i}^T}$ 또는 $\frac{1}{n}{x_i}^Tx_i$ 로 표현할 수 있다.
두 식 중에서 후자의 경우가 더 계산이 빠르다.

span, basis 등

• span(A) : 행렬 A의 벡터로 만들 수 있는 모든 것
• generating set : span(A)가 vector space를 전부 표현할 때의 행렬 A
• basis : 모든 linearly independent한 generating set
• dimension : basis 집합의 크기

row space, column space

Ax = 0일 때,

• row space는 null space와 orthogonal
• col space는 left null space와 orthogonal
• col space는 range matrix라고도 불린다.

rank

• linearly independent한 col의 개수, row의 개수
• dim(rowspace(A)), dim(colspace(A)), dim(basis)
• A가 invertible하면 rank(A)=n

linear map, kernel, image

• linear map
  • 
• kernel : null space
  • 
• image : $\Phi$(x)가 만들 수 있는 y의 집합
  • 
• kernel-image
  •