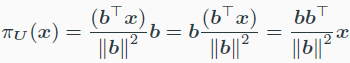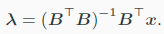본 포스팅은 AI501 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

---

Norm

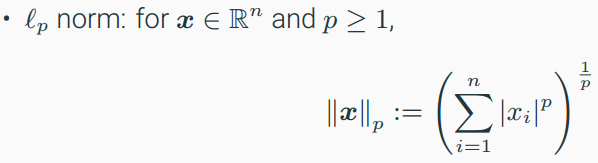
• l2 norm : 계산, 최적화 쉬움, dl에서 weight decay에 사용
• l1 norm : sparsity inducing norm, sparsifying 문제일때 사용, LASSO 알고리즘에서 사용
• $l_{\infty}$ : x1, …, xn까지 중에 가장 긴 vector
• l0 norm : norm 아님, x의 non-zero element의 개수

vector norm

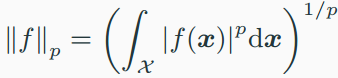
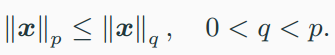
matrix norm

• Matrix의 complexity를 측정할 때, Regularizae를 통해 robust model을 만들 때 사용

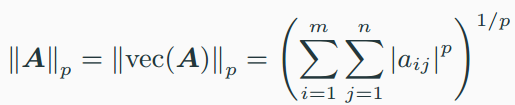
• Frobenious norm
  • matrix의 l2 norm을 의미하고, optimization 문제에서 사용됨
  • 특히 중요함, A의 singular value들의 제곱의 합을 의미

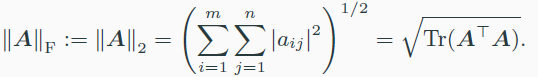
induced norm

• 벡터의 놈에서 유도된 행렬의 놈

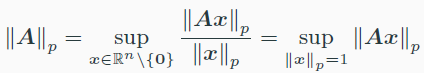
• $\lVert A\rVert_1$ 은 maximum col sum of A
• $\lVert A\rVert_\infty$ 은 maximum row sum of A
• $\lVert A\rVert_2$ 은 largest singular value of A
• Schatten norm? : matrix p-norm을 singular value로 계산하는 것?
  • $\lVert A\rVert _1$ 은 nuclear norm
  • $\lVert A\rVert _\infty$ 은 spectral norm
  • $\lVert A\rVert _2$ 은 frobenius norm

inner product

• $\lVert x\rVert=\sqrt{<x,x>}$
• dot product는 inner product의 일종이다.
• 코시-슈파르츠
  • $<x,x>^2 \leq <x,x><y,y>$

positive definite matrix

• positive definite matrix : $x^TAx\gt0$
• positive semi-definite matrix : $x^TAx\geq0$
• positive definite하면 $<x,y>=x^TAy$ 이고, $A=LL^T$로 cholesky decomposition할 수 있다. 여기서 L은 lower-triangular matrix + positive diagonal entries 이다.

Metric (distance)

• $d(x,y)=\lVert x-y\rVert=\sqrt{<x-y,x-y>}=\sqrt{(x-y)^TA(x-y)}=\sqrt{(x-y)^TLL^T(x-y)}$
• metric learning : 위 식에서 positive definite matrix A 또는 L을 를 학습하는 것

Orthogonality

• $Q^TQ=QQ^T=I$
• $\frac{<Qx,Qy>}{\lVert Qx\rVert\lVert Qy\rVert}=\frac{<x,y>}{\lVert x\rVert\lVert y\rVert}$ orthogonal matrix는 vector의 angle을 유지한다.

Projection

• Projection matrix P 는 idempotent($P^2=P$)이다.
• Orthogonal projection matrix : $P^2=P=P^T$
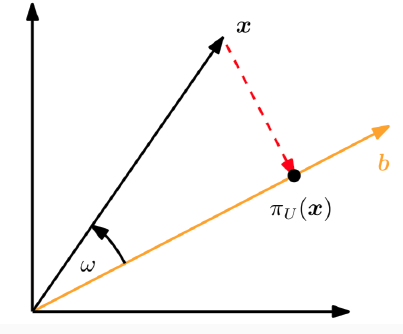
• line에 projection
  • 
  • 
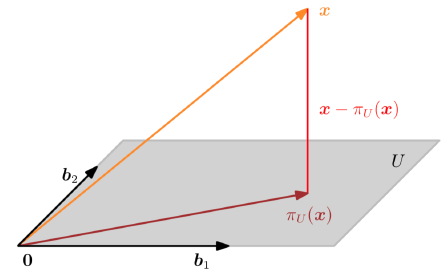
• space에 projection
  • 
  • 
  • 
• pseudo-inverse
  • $(B^TB)^{-1}B^T$를 말한다.
  • non-square matrix의 inverse의 일반화
  • B는 full column rank이다.