본 포스팅은 AI501 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

---

determinant

• det(A) 값은 unit square을 A로 transform 했을 때의 area를 의미한다.
• $det(A)\not ={0}$ 이면 A는 full rank이다.

eigenvalue, eigenvector

$Ax=\lambda x$

• $det(Ax-\lambda x)=0$
• $rank(Ax-\lambda x)<n$
• 왜냐하면 det=0이면 full rank가 아니다.
• eigenvector는 A로 transform 했을 때 바뀌지 않는 방향이고, eigenvalue는 scale을 의미한다.

Algebraic multiplicity vs Geometric multiplicity

• characteristic polynomial of A
  • $p_A(\lambda)=det(A-\lambda I)$
• Algebraic multiplicity
  • $p_A(\lambda)$에서 root로 몇번 나오는지가 algebraic multiplicity이다.
• Geometric multiplicity
  • eigenspace($E_\lambda$)는 $A-\lambda I$의 null space. $E_\lambda$의 차원이 geometric multiplicity
• 다른 eigenvalue를 갖는 eigenvector는 linearly independent하다.
• $1\leq geometric\;multiplicity\leq algebraic\;multiplicity\leq n$

eigenvalue, eigenvector의 성질

• $det(A)=\Pi_{i=1}^n\lambda_i$ : eigenvalue의 곱
• $Tr(A)=\Sigma_{i=1}^n\lambda_i$ : eigenvalue의 합
• Hermitian(symmetric for real)의 eigenvalue는 real
• triangular matrix의 eigenvalue는 diagonal elements
• Principle component analysis에서 eigenvector 사용한다.

Diagonalizable Matrix

$A=X\Lambda X^{-1}$ 로 표현가능 할 때, A는 diagonalizable하다.

• $AX=X\Lambda$
• $Ax_i=\lambda_ix_i$ ($x_i$는 col vector)
• A가 n개의 linearly independent한 eigenvector를 가질 때, A는 diagonalizable하다.
• nxn 행렬이 n개의 eigen value 가질 때 diagonalizable하다.
• nxn 행렬은 geometric multiplicy가 algebraic multiplicy와 같을 때 diagonalizable하다.
• diagonalizable이 invertible한 것은 아니다.

Eigen decomposition

정사각행렬 A는 $A=X\Lambda X^{-1}$ 을 만족한다.

• X는 column에 eigenvector를 가짐
• $\Lambda$ 는 eigenvalue를 값으로 가지는 diagonal matrix

Singular value decomposition

$A=U\Sigma V^T$

U와 V는 orthogonal matrix이고, $\Sigma$는 singular value로 이루어진 diagonal matrix이다.

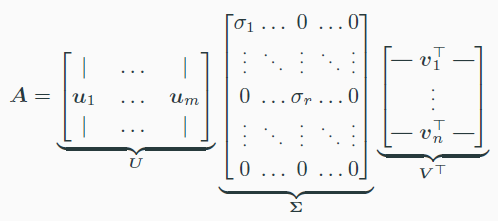
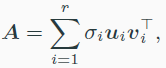
위와 같이 나타낼 수 있다. 여기서 convention으로 $\sigma_1\geq\sigma_2\geq…\gt 0$이다.

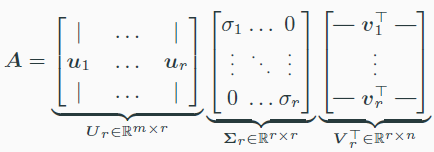
compact하게 만들 수도 있다.

• SVD가 eigen decomposition과 관련이 있는 이유

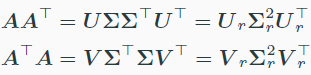
$AA^T$의 eigen vector가 U이고, eigen value가 ${\Sigma_r}^2$ 이다.

• ML에 활용하는 방법 : low-rank approximation (너무 작은 eigen value는 삭제), denoise효과

SVD and matrix norm

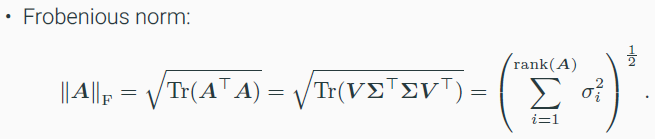
• Frobenious norm : element-wise l2 norm
• Spectral norm : 가장 큰 singular value