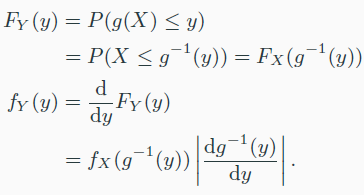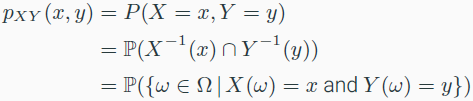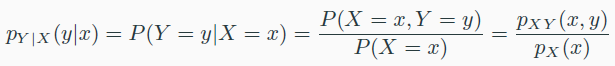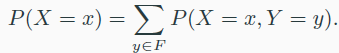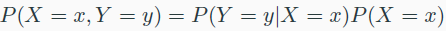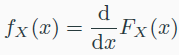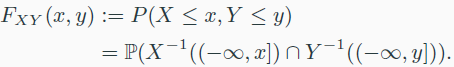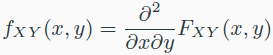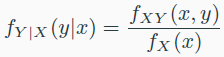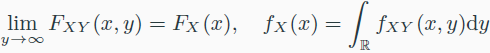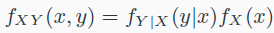본 포스팅은 AI501 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

---

Bayesian probability

1. 주사위를 던져 0이 나올 사전 확률을 가정한다.
2. 주사위를 많이 던져서 확인해본다.
3. 실험 결과가 사전확률과 다르다면 사전확률을 수정하여 사후확률을 계산한다.

• degree of belif
• 확률값은 고정된 상수가 아닌 분포, 확률 변수이다.
• 데이터가 변화하면, 확률 변수를 최대화하는 분포도 계속 변화할 수 있다.
• 사전확률을 이용할 수 있다는 장점
• Frequentist probability에서는 데이터를 설명하는 파라미터는 고정되어있고, 데이터는 그 파라미터가 맞는지 틀린지 확인하는 도구로써의 역할
• Bayesian probability에서는 가지고 있는 데이터를 가장 잘 설명하는 어떤 확률분포, 확률 모델을 잘 찾아나가는 데에 목표

청바지를 생산하는 공장이 3군데 있다. 불량청바지가 나왔을 때, 청바지가 어떤 공장에서 생산된 것인지(사후 확률)을 3개의 공장의 불량률(사전 확률)을 이용하여 구하고 싶다.

Probability

• sample space $\Omega$: 모든 결과
• set of events $F$ : 일어날 수 있는 모든 event의 집합, $\Omega$의 power set
• Probabiliy measure $P:F→[0,1]$

Random variable

• probability space에서 measure space로의 measurable mapping
• probability space($\Omega, F, P$), target space ($E$)
• $E$ 는 모든 가능한 random variable의 집합이다.
• $\epsilon$ (probability space($E$))의 subset의 power set) 는 E의 power set이 아니다. 그리고 $\sigma$-algebra라는 조건을 따른다.
• 

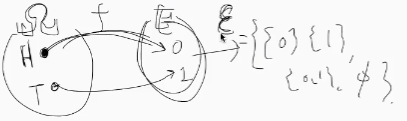
Discrete Random Variable

• X는 random variable이고, target space E 가 discrete
• Probability mass function(pmf)
  • $p_x(a) = P(X^{-1}({a}))$
  • $P(X\in A)=\Sigma_{x\in A}P(X=x)=\Sigma_{x\in A}p_X(x)$
• joint pmf
  • 
• conditional probability
  • 
• marginalization
  • 
• product rule
  • 

Continuous random variable

• random vriable이 continuous target space에서 정의되는 경우
• Borel $\sigma$-algebra 조건을 갖는다.
• Cumulative Distribution Function(CDF)
  • 
  • 
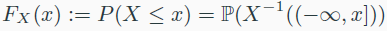
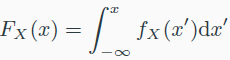
  • right-continuous
• Probability Density Function(PDF)
  • 
• joint CDF
  • 
• joint PDF
  • 
• conditional pdf
  • 
• sum rule
  • 
• product rule
  • 
• IID(independent and identically distributed) 이면 joint pmf, joint cmf가 아래와 같다. joint pdf도 마찬가지이다.
  • 
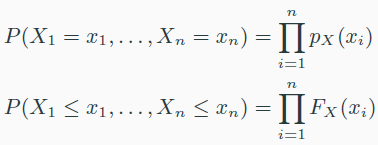
  • log를 하면 계산이 쉽다.

Bayes’ Rule

• 
• 
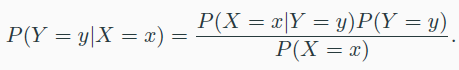
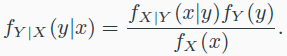
• Bayes’ Rule이 statistical machine learning에 사용되는 예시
  • $\theta$ 로 parameterized된 모델은 아래와 같다.
  • 
  • 
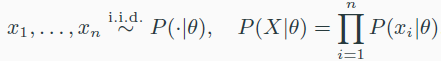
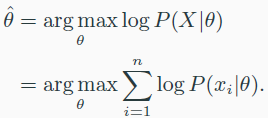
  • F($x_*,\hat{\theta}$)로 inference
• control이 어려운 random variable에 대한 확률을 구할 수 있다.

Covariance

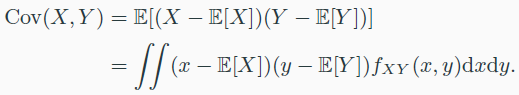
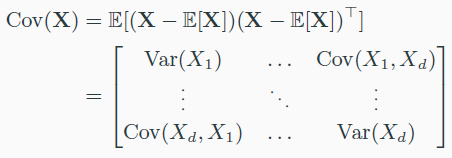
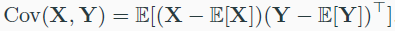
Law of total variance

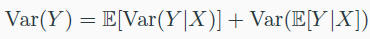
• MC dropout

Inverse transform sampling (sampling technique)

$F_X$ 가 cdf 이고, $U \sim Unif(0,1)$일 때,

$F_U(u) = u$

$P(F_X^{-1}(u) \leq x) = P(u \leq F_X(x)) = F_U(F_X(x))= F_X(x)$

$F_X^{-1}(U)$ 가 $F_X$의 cdf를 가진다는 의미이다.

따라서 ramdom sampling을 할 때, $x=F_X^{-1}(u)$ 를 사용한다.

Change of variables

만약 Y=g(x)라면,