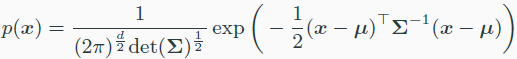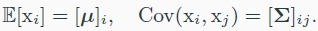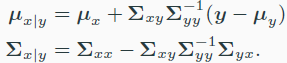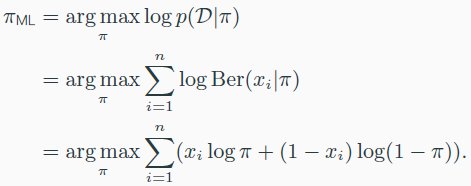(AI501) 7. Commonly used probability distributions
본 포스팅은 AI501 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.
Notation
| Symbol | example | Description |
|---|---|---|
| roman, lowercase | $\mathrm{x}$ | scalar rv |
| italic, lowercase | $x$ | $\mathrm{x}$의 실제 값 |
| roman, bold, lowercase | $\mathbf{x}$ | vector rv |
| italic, bold, lowercase | $\mathrm{\boldsymbol{x}}$ | $\mathbf{x}$의 실제 값 |
| roman, uppercase | $\mathrm{X}$ | matrix rv |
| italic, uppercase | $X$ | $\mathrm{X}$의 실제 값 |
pdf, pmf는 lower-case로 적는다.
Gaussian distribution
가우시안 분포를 쓰는 이유
- CLT : iid RV일때 가우시안 분포로 수렴한다.
- Maximizing entropy : 어떤 시스템이 $\mu$, $\sigma$를 가진다면 이것을 가장 maximize하는 것은 gaussian 분포
- entropy는 degree of spread out을 의미한다.
- entropy가 가장 큰 것은 uniform이고, 가장 작은 것은 delta이다.
- 계산이 쉽다.
- jointly multivariate gaussian
- jointly multivariate gaussian
-
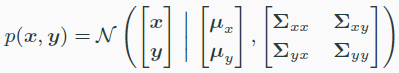
- 위와 같은 상황에서 $p(x\rvert y)$도 가우시안 분포$N(x\rvert \mu_{x\rvert y},\Sigma_{x\rvert y})$를 따른다.
- marginal distribution도 가우시안 분포를 따른다.
-
- x와 y가 independent한 가우시안일 경우 linear combination도 가우시안이다.
Bernoulli distributions
- p(x=1)=$\pi$, p(x=0)=1-$\pi$
- E[x]=$\pi$, Var[x]=$\pi(1-\pi)$
- maximum likelihood
- Bayesian에선 $\pi$를 random variable로 다룬다.
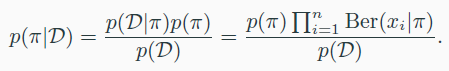
- p($\pi$) : prior distribution, data를 보기 전에 가정
- p($\pi\rvert D$) : posterior distribution, 실제 data를 봤을 때, $\pi$의 확률
- p(D) : marginal likelihood