본 포스팅은 AI501 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

Beta distribution

• 확률에 대한 확률
  • a,b가 결과로 나왔을 때, a가 나올 확률이 $\pi$일 확률
• a와 b는 양수이다.
• 팩토리얼의 일반화
• 
• 
• 
• 
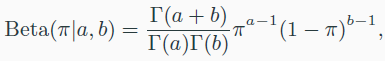
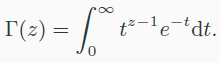
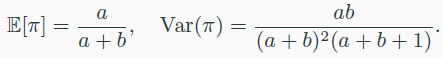
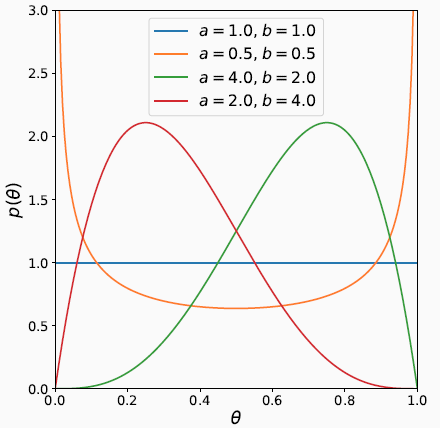
  • b가 커지면 0에 치우쳐짐
  • a,b가 커지면 위로 높아짐
  • a,b가 작다면 아래로 낮아짐
  • a = 1, b = 1이면 1
• beta distribution은 bernoulli distribution의 conjugate prior이다. (conjugacy, 둘은 conjugate pair)
  • bernoulli likelihood + beta prior $\rightarrow$ beta posterior

Binomial distribution

• 
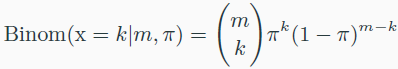
• bernoulli 분포를 따르는 m개의 data의 합은 binomial distribution을 따른다.
• Beta distribution은 binomial distribution의 conjugate prior (with parameter π)

Categorical distribution

• 주사위를 한번 던질 때, 3이 나올 확률
• 

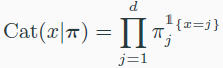
Multinomial distribution

• 주사위를 m번 던질 때, y가 나올 확률
• 

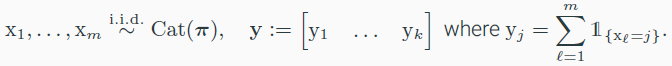
Dirichlet distribution

• Beta distribution을 다항분포 형태로 확장시킨 분포이다.
• Categorical distribution, Multinomial distribution의 $\pi$의 prior distribution
• 가위바위보를 할 때, 만약 친구가 가위를 a번 주먹을 b번 보를 c번 냈다. 이때 확률이 0.25, 0.25, 0.5일 가능도가 Dir(0.25,0.25,0.25;a,b,c)이다.
• 
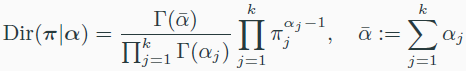
• dirichlet distribution은 categorical distribution과 multinomial distribution의 conjugate prior이다.
  • categorical likelihood + dirichlet prior $\rightarrow$ beta posterior

Gamma distribution

• 
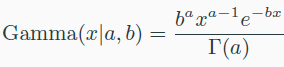
• $\alpha$ : shape parameter, $\alpha$ 개의 사건이 일어날 때까지의 대기시간
• $\beta$ : rate parameter, 평균 소요시간
• 감마 분포를 따르는 샘플을 normalize하면 dirichlet 분포를 따른다.

Gaussian의 conjugate prior