본 포스팅은 AI501 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

constrained optimization

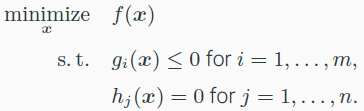
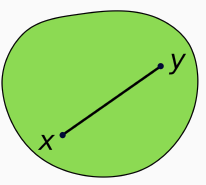
Convex sets

• 
• 

• local minimum = global optimum

• convex set
  • empty set, singleton set, entire spae $R^d$
  • norm ball
  • hyperplane
  • halfspace
  • Affine transform
• convex set 특징
  • 
• convex function
  • constant function
  • exponential
  • power function of absolute value
  • pointwise max function
  • log-sum-exp(soft-version of max) : 확률이 너무 작아서 log 취함
  • affine function
  • quadratic function
• convex function 특징
  • 

Convex optimization problems

• 
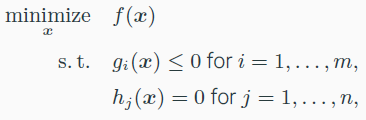
• f, g 가 convex하고, h가 affine일 때, Convex optimization problems이다.
• feasible set : 모든 constraints를 만족하는 optimization variable 집합

Lagrangian and Lagrange multipliers

• primal problem
  • 
• Lagrangian
  • 
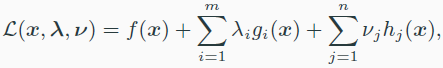
  • Lagrangian multiplier : $\lambda, \nu$
• 
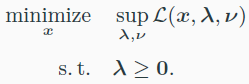
  • 조건을 안지키면 $\inf$가 됨
  • $\lambde$가 0일 때 제일 큼(supremum)