본 포스팅은 AI502 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

---

Bias와 Variance

Bias

• $Bias[h(x)]=\bar{h(x)}-f(x)$
• Bias는 추정값의 평균과 실제 값의 차이
• Bias가 생기는 이유
  • decision boundary를 표현할 수 없음.
  • 잘못된 추정
  • model이 global, smooth함.
  • underfitting

Variance

• $Var[h(x)]=E[(h(x)-\bar{h(x)})^2]$
• 분산
• Variance가 생기는 이유
  • local
  • sharp decision boundary
  • randomization(학습 처음 시작할 때)
  • overfitting

Bias-Variance Decomposition

$E[(y-h(x))^2]=E[(h(x)-\bar{h(x)})^2]+(\bar{h(x)}-f(x))^2+E[(y-f(x))^2]$

Error = Variance + Bias^2 + Noise

Bagging

다른 sample들로 학습한 여러 모델들로 추론하고 평균내는 방법

Regularization

bias를 증가시키고, variance를 줄이는 방법

Singular Value Decomposition(SVD)

$A=U\Sigma V^T$, U와 V는 orthogonal, $\Sigma$는 singular value로 구성된 diagonal matrix

Multivariate Linear regression

• $\theta^{OLS}=min_{\theta}\lVert y-\theta\rVert_2^2=<y-X\theta,y-X\theta>=(y-X\theta)^T(y-X\theta)$

• $\theta=(X^TX)^{-1}X^Ty$ : normal equation

• $X^TX$ : normal matrix

Probabilistic interpretation

likelihood function : 주어진 X,yi에 대한 $\theta$의 분포

• 
• 
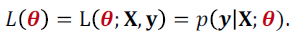
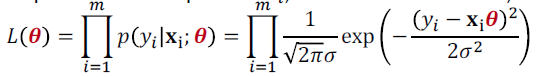
• probabilistic model에서 likelihood를 maximize하는 $\theta$를 찾아야한다.
• 2번째 식을 log likelihood로 바꿔서 식을 전개하다 보면 minimizing RSS로 바뀐다.

Ridge Regression

• L2-regularization을 쓰는 Linear regression
• 
• 
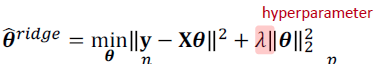
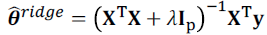
• $\lambda$가 0이면 $\hat{\theta}^{ridge}=\hat{\theta}^{OLS}$
• PRSS라고도 표현한다.

cross-entropy loss

• 
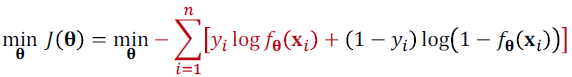
• yi와 f(x)간의 cross-entropy
• convex하다.
• 

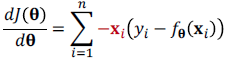
sgd

• batch, deterministric gradient descend : 모든 training set 사용
• stochastic gradient descend : 일부 sample 사용
• minibatch size는 중요하다.
  • large batch는 더 accurate
  • multicore architecture는 주로 small batch로 충분히 활용되지 않는다. 이때는 processing time이 줄어들지 않는 범위 내에서 batch size를 키운다.
  • 몇몇 hardward은 $2^k$ size를 가질 때 runtime이 좋다.
  • small batch는 regularizing 효과가 있다.
• 장점
  • 더 빠르게 수렴
  • local minima 문제를 해결한다.

Newton’s method

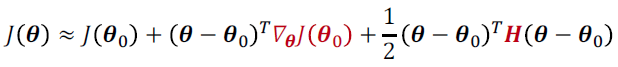
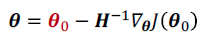
Hessian Matrix