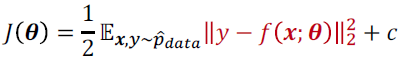본 포스팅은 AI502 수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

cost function

• negative log-likelihood
  • 
• MSE
  • 
• cost function : maximum likelihood
  • $-logp(y\lvert x)$
  • 

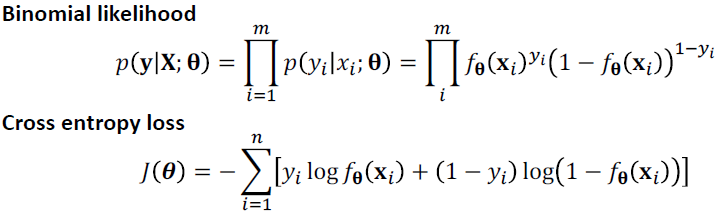
여러가지 unit, activation 함수

• gaussian mixture?
• absolute value rectification
  • $g(z)=\lvert z\lvert$
• maxout
  • g(z)=max $z_j$
• softplus
  • $\sigma(z)=log(1+e^z)$
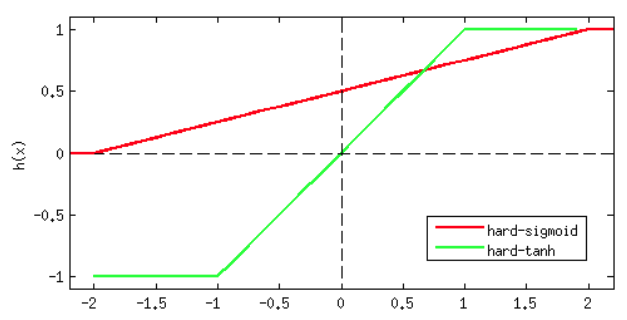
• hard-tanh, hard-softmax
  • 

Weight initialization

• weight initialization은 주로 limited range에서 randomly하게 정해진다.
  • 값이 너무 크면 explode되고, 너무 작으면 vanishing 한다.
  • random initialization이 중요한 이유는 학습된 feature의 redundancy와 correlation을 줄일 수 있기 때문 (break symmetry)
• initialization
  • fan-in 개수와 fan-out 개수
  • non-linear activation function의 종류, network의 종류
• batchnorm을 쓰면서부터 initialization에 덜 sensitive하다. batchnorm은 scale과 shift를 학습한다.
• LeCun Weight Initialization
  • 
• Xavier Weight Initialization
  • 
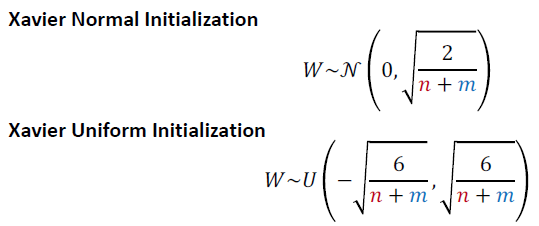
  • Relu와 쓰면 activation이 0이 된다.
• He Weight Initialization
  • 
  • Relu와 같이 쓴다.

Training Deep feedforward networks

• 학습하는 것은 computation & memory cost가 많이 든다.
  • forward propagation 할 때 O(w)(w는 weight의 개수) 만큼 multiply-add를 한다.
  • backward propagation 할 때, 각 weigth matrix의 transpose를 곱해야 한다.
  • memory cost가 $O(mn_h)$, m은 minibatch 의 크기, $n_h$는 hidden unit의 개수
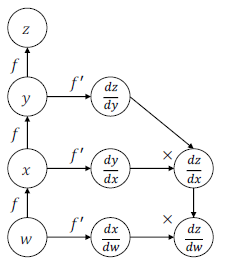
• computational graph
  • 각 노드에 gradient를 저장함으로 효율적이다.
  • 

Why Deep network work better

• Universal approximate theorem
  • 적어도 하나의 hidden layer와 squashing activation function으로 어떤 continuous function이든 만들 수 있다.
  • 
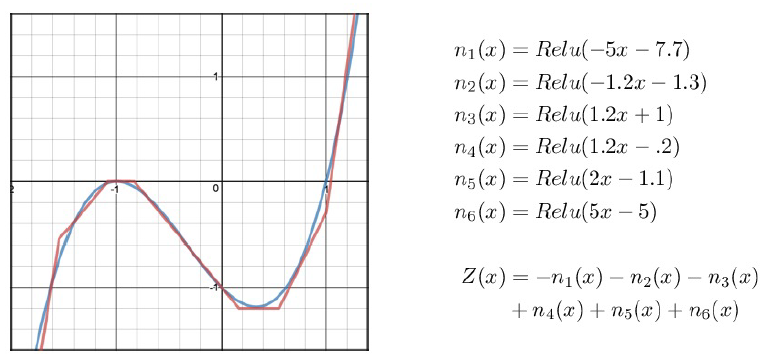
  • 하지만 network가 얼마나 커야하는지 모른다.
  • 네트워크 크기의 bound를 제안하는 것도 있었지만, hidden unit이 exponential하게 필요하기 때문에 더 좋지 않았다.
  • 모든 continuous function을 표현한다고 해도 아주 큰 네트워크가 필요하거나 학습을 실패하거나 generalize를 실패하였다.
  • deeper model을 쓰면 unit의 사이즈를 줄일 수 있고, generalization error를 줄일 수 있었다.
    
    
• deep model이 더 accurate하다.
• deep model은 input space를 fold하는 것과 비슷하다. layer의 depth에 exponential하게 linear region의 수가 증가한다.
• 결국 우리가 학습하려는 것은 많은 단순한 function들로 구성된 function
• 경험상 depth가 크면 generalization이 잘 된다.