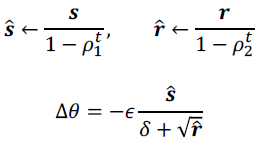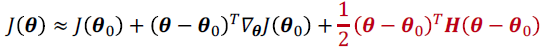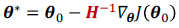본 포스팅은 AI502수업에서 제가 새로 알게 된 부분만 정리한 것입니다.

---

Convex Optimization problem

$f(\theta x + (1-\theta) y) \leq \theta f(x)+(1-\theta)f(y)$

• global optimum
• reliable & efficient algorithms

Taylor series Approximations

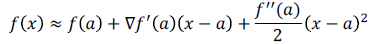
Surrogate Loss Function

• 0-1 loss 처럼 gradient 없는 함수의 proxy

minibatch 사용하는 SGD

• regularization effect
• multicore architecture에서 batch 크기가 작으면 제대로 활용x

Neural network optimization의 한계

• III-conditioning : critical point에 도달x
• Local minimum $\neq$ Global minimum
• Linear path experiments
• plateau, saddle point, flat regions
• gradient clipping
• long term dependecies
  • vanishing
  • exploding

learning rate

• convergence condition
  • 
  • 
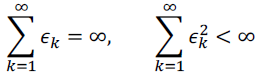
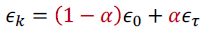
    • $\epsilon_{\tau}$ 는 $0.01\times \epsilon_{o}$
• convex problem : $O(\frac{1}{\sqrt(k)})$
• strong convex problem : $O(\frac{1}{k})$

Cyclic Learning Rate

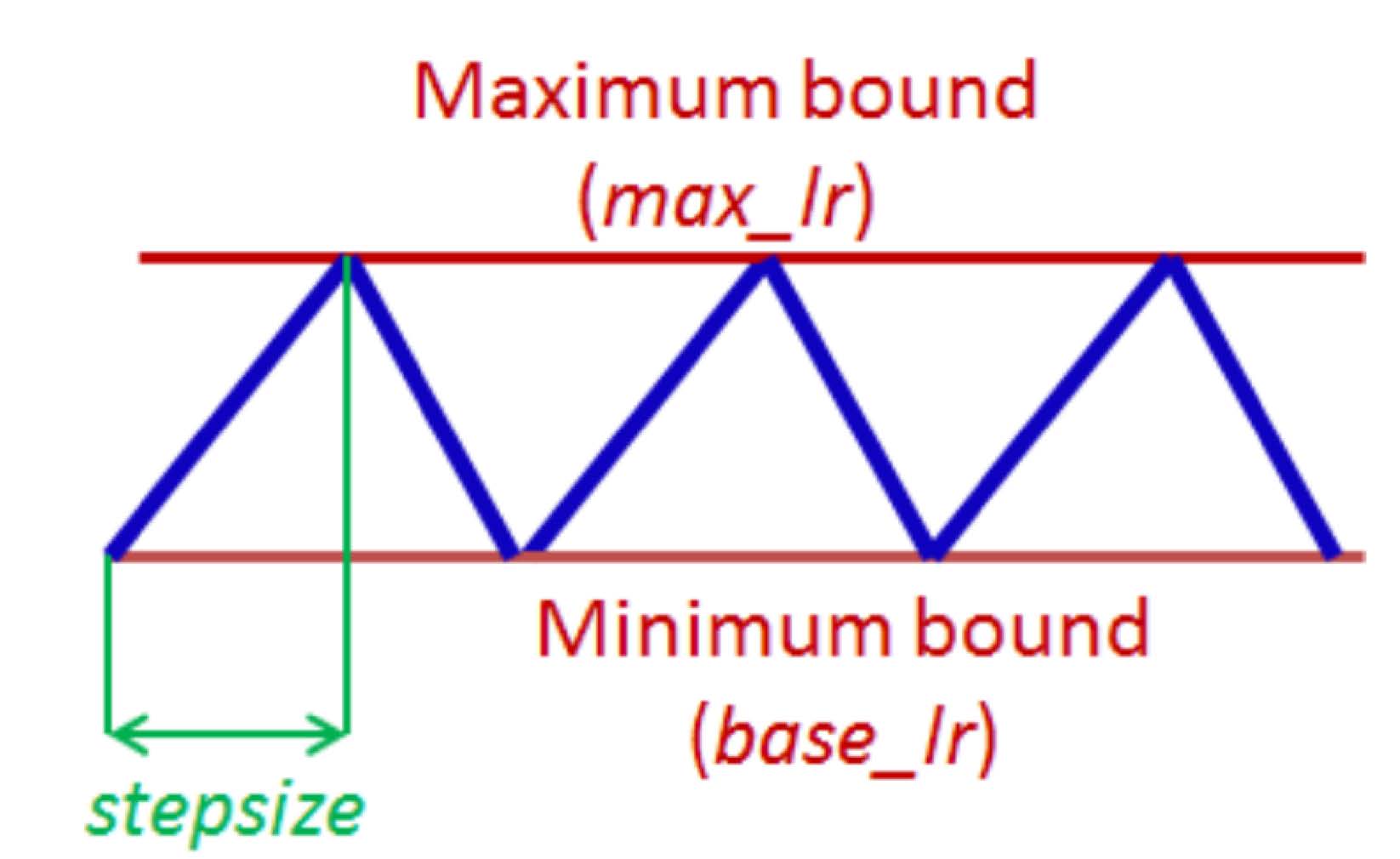
Momentum

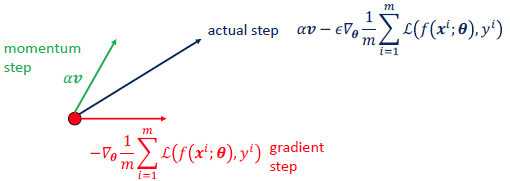
• $\alpha$가 크면 이전 gradient의 효과가 커진다.
• 2 문제 해결
  • poor conditioning of hessian matrix
    • 
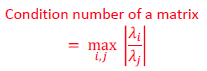
    • condition number가 낮아지면, gradient descent를 잘 못한다. 한쪽방향으로의 derivative가 빠르게 증가하기 때문에
    • 타원형
  • variance in stochastic gradient

Nesterov Momentum

• current velocity가 계산된 후에 gradient를 계산함.
• 
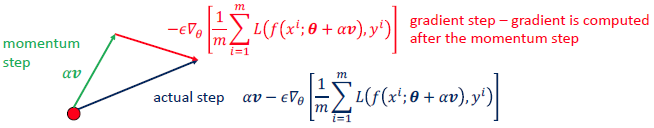
• strong convex problem : $O(\frac{1}{k^2})$

Initialization

• break symmetry
  • large initial weights는 효과가 크다
• randomly하게 정해짐(Gaussian, uniform)
• random orthogonal matrices
• Adaptive Learning Rates : learning rate를 큰 것과 작은 것을 섞어서 사용
• AdaGrad : separate learning rate
  • 
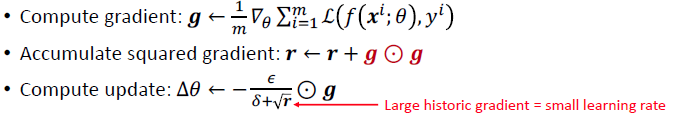
    • gradient가 크면 learning rate가 크게 줄어듦
    • gradient가 작으면 learning rate가 작게 줄어듦
• RMSProp
  • 
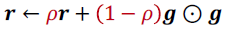
  • 계속 줄어드는 것을 막음
  • 이전 기록에서 얼마나 기억할지 $\rho$0
• Adam
  • RMSProp + momenturm
  • 
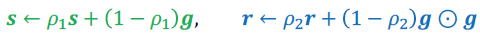
  • bias correction
    • 

Approximate Second-Order Methods

• newton’s method
  • 
  • 
• damped newton
  • Attacking Saddle Point Problem
  • 
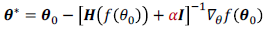
  • $\alpha$가 크면 gradient descent랑 비슷해지고, 빠르게 수렴하는 장점이 사라진다.
• Saddle-Free Newton’s Method
  • 
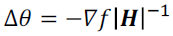
  • ignore negative curvature
• Broyden-Fletcher-Goldfarb-Shanno(BFGS)
  • newton’s method 비슷하게 만든 것
  • Hessian을 추정하기 위해서 최근 iteration의 curvature을 사용
  • $H^{-1}$을 대신하여 M을 사용
    • 
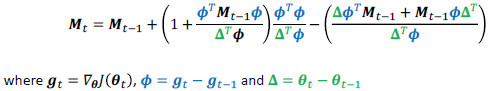
    • $O(d^2) time, memory$
• Limited-Memory BFGS
  • $M^{t-1}$을 identity matrix로 바꿔서 mamory cost를 크게 줄임.
  • 

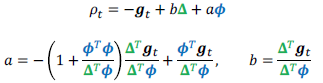
Optimization Strategies and Meta-Algorithms

• Coordinate Descent
  • 한번에 1개의 variable만 optimize
  • 여러 variable이 서로 연관되어 있으면 성능 안좋다.
• Polyak averaging
  • parameter trajectory에 있는 여러 점을 평균
  • convergence 보장
  • non-convex일 때
    • exponentially decaying average를 사용
• Supervised Pretraining
  • simpler model을 학습하는 것
  • step by step으로
• continuation methods
  • smooth the objective
• curriculum learning
  • 쉬운 것부터 어려운 것 학습