본 포스팅은 아래 포스팅을 정리한 것입니다.
https://hyunw.kim/blog/2017/10/27/KL_divergence.html
정보량
26개의 알파벳에서 6개의 알파벳을 맞추려면
$2^{질문개수} = 26$
$질문개수 = 6 \times log_2(26(가능한 결과의 수))$
$H=nlog(s)$
Entropy
- A : 0.5, B : 0.125, C : 0.125, D : 0.25
이때, A인가? D인가? B인가? 순으로 묻는게 가장 효율적이다. 이것으로 평균적으로 1.75개의 질문을 하는 것을 알 수 있다.
$P(A)\times 1 + P(B)\times 3 + P(C)\times 3 + P(D)\times 2 = 1.75$
- 그리고 발생 확률로 질문의 개수를 알 수 있다.
- $log_2(\frac{1}{1/2})=1$, $log_2(\frac{1}{1/8})=3$, $log_2(\frac{1}{1/4})=2$
- A : 0.25, B: 0.25, C: 0.25, D : 0.25
이것은 AB인가? A C인가? 로 질문하는게 효율적이고, 이것은 평균 2개의 질문을 하게 된다.
평균 1.75개의 질문을 하는 것
- 더 적은 정보량
- 불확실성(랜덤성)이 적기 때문
- 이런 불확실성이 Entropy
모든 사건이 일어날 때 엔트로피는 최대값을 가짐.
이산확률분포일때, $H=\Sigma p_i log_2(\frac{1}{p_i}) = -\Sigma p_i log_2(p_i)$
Cross Entropy
P : A : 0.5, B : 0.125, C : 0.125, D : 0.25 Q : A : 0.25, B: 0.25, C: 0.25, D : 0.25
Q 전략을 P에 적용하면? $0.5\times 2+0.125\times 2+0.125\times 2+0.25\times 2 = 2$
1.75에서 0.25가 증가
따라서 특정 전략을 사용할 때의 기대값을 의미한다.
$H(p,q)=-\Sigma p_i log_2(q_i)$
$H(p,q)=-\int p_i log_2(q_i)$
Binary classification & Cross entropy(?)
p = [y, 1-y]
q = [$\hat{y}$,1-$\hat{y}$]
$-ylog\hat{y}-(1-y)log(1-\hat{y})$ (?)
KL divergence
- 두 확률분포의 차이를 계산하는 데 사용하는 함수
- 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링 하면 발생할 수 있는 정보 엔트로피 차이를 계산한다.
- $KL(p\lVert q)=H(p,q)-H(p)$
- KL $\geq$ 0이다. Jensen’s inequality(convex한 함수)
- 거리 개념이 아니고, asymmetric하다.
Jensen-Shannon divergence
$JSD=\frac{1}{2}KL(p\lVert M)+\frac{1}{2}KL(q\lVert M), where M = \frac{1}{2}$
KL divergence 활용
- 알 수 없는 분포 p(x)에서 추출되는 데이터로 모델링을 하려고 한다.
- $q(x\lvert \theta)$로 근사시키려고 할 때, p(x)와의 KL-divergence를 최소화하는 parameter $\theta$를 찾는 것.
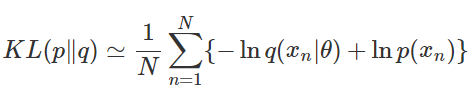
이해 안되는 내용
- cross-entropy minimize, log likelihood maximize
- KL-divergence minimize, log likelihoode maximize